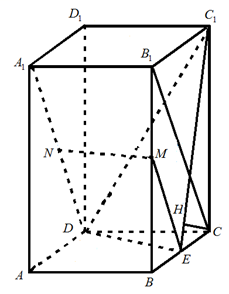
（1）连结\[{{B}_{1}}C,ME\].因为M，E分别为\[B{{B}_{1}},BC\]的中点，所以\[ME\text{ }\parallel \text{ }{{B}_{1}}C\]，且\[ME=\frac{1}{2}{{B}_{1}}C\].又因为N为\[{{A}_{1}}D\]的中点，所以\[ND=\frac{1}{2}{{A}_{1}}D\].

由题设知\[{{A}_{1}}{{B}_{1}}\parallel \text{=}DC\]，可得\[{{B}_{1}}C\parallel \text{=}{{A}_{1}}D\]，故\[ME\parallel \text{=}ND\]，因此四边形MNDE为平行四边形，\[MN\parallel ED\].又\[MN\not\subset \]平面\[{{C}_{1}}DE\]，所以MN∥平面\[{{C}_{1}}DE\].

（2）过C作C₁E的垂线，垂足为H.

由已知可得\[DE\bot BC\]，\[DE\bot {{C}_{1}}C\]，所以DE⊥平面\[{{C}_{\text{1}}}CE\]，故DE⊥CH.

从而CH⊥平面\[{{C}_{1}}DE\]，故CH的长即为C到平面\[{{C}_{1}}DE\]的距离，

由已知可得CE=1，C₁C=4，所以\[{{C}_{1}}E=\sqrt{17}\]，故\[CH=\frac{4\sqrt{17}}{17}\].

从而点C到平面\[{{C}_{1}}DE\]的距离为\[\frac{4\sqrt{17}}{17}\].